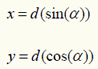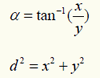2.0 Introduction
Different kind of coordinates are used to position objects in a two- or three-dimensional space. Spatial coordinates (also known as global coordinates) are used to locate objects either on the Earth’s surface in a 3D space, or on the Earth’s reference surface (ellipsoid or sphere) in a 2D space. Specific examples are the geographic coordinates in a 2D or 3D space and the geocentric coordinates, also known as 3D Cartesian coordinates. Planar coordinates on the other hand are used to locate objects on the flat surface of the map in a 2D space. Examples are the 2D Cartesian coordinates and the 2D polar coordinates.
2.1 2D geographic coordinates (f,l)
The most widely used global coordinate system consists of lines of geographic latitude (phi or f or j) and longitude (lambda or l). Lines of equal latitude are called parallels. They form circles on the surface of the ellipsoid. Lines of equal longitude are called meridians and they form ellipses (meridian ellipses) on the ellipsoid. Both lines form the graticule when projected onto a map plane. Note that the concept of geographic coordinates can also be applied to a sphere as the reference surface.
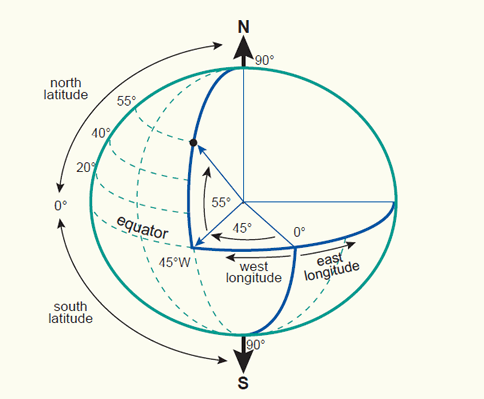
The latitude (f) and longitude (l) angles represent the 2D geographic coordinate system.
The latitude (f) of a point P (figure section 2.2) is the angle between the ellipsoidal normal through P' and the equatorial plane. Latitude is zero on the equator (f = 0°), and increases towards the two poles to maximum values of f = +90 (90°N) at the North Pole and f = - 90° (90°S) at the South Pole.
The longitude (l) is the angle between the meridian ellipse which passes through Greenwich and the meridian ellipse containing the point in question. It is measured in the equatorial plane from the meridian of Greenwich (l = 0°) either eastwards through l = + 180° (180°E) or westwards through l = -180° (180°W).
Latitude and longitude represent the geographic coordinates (f,l) of a point P' (figure section 2.2) with respect to the selected reference surface. They are also called geodetic coordinates or ellipsoidal coordinates when an ellipsoid is used to approximate the shape of the Earth. Geographic coordinates are always given in angular units. An example, the coordinates for the City hall in Enschede are:
f = 52° 13' 26.2" N, l = 6° 53' 32.1" E.
These latitude and longitude coordinates are related to the Amersfoort datum. Note that the use of a different reference surface will result in a different latitude and longitude (section 5.2 on datum transformations).
There are several formats for the angular units of geographic coordinates. The Degrees:Minutes:Seconds (49°30'00"N, 123°30'00"W) is the most common format, another the Decimal Degrees (49.5000°, -123.5000°), generally with 4-6 decimal numbers. A tool for the conversion of geographic coordinates between Degrees:Minutes:Seconds and Decimal Degrees (external link):
Geographic coordinates are often used to store and manage, and interchange spatial data. The data are projected onto a local map coordinate system for editing, analysis and mapping. As example, the internal coordinate system of Google Earth are geographic coordinates (latitude/longitude) on the World Geodetic System of 1984 (WGS84) datum. When the data are displayed on the monitor they are projected using the equidistant cylindrical (or simple cylindrical) map projection.
Next to the geodetic (or geographic) latitude (f) there are two other type of latitudes. These are the astronomic latitude and the geocentric latitude. The astronomic latitude (F) (figure below) is the angle between the equatorial plane and the normal to the Geoid (i.e. a plumb line). It differs from the geodetic (or geographic) latitude only slightly, due to the slight deviations of the Geoid from the reference ellipsoid. The astronomic latitude is the latitude which results directly from observations of the stars, uncorrected for vertical deflection (section 3.5), and applies only to positions on the Earth's surface. Astronomic observations are used to establish local horizontal (or geodetic) datums. The geocentric latitude (f') is the angle between the equatorial plane and a line from the center of the ellipsoid (used to represent the Earth). This value usually differs from the geodetic latitude, unless the Earth is represented as a perfect sphere. Both geocentric and geodetic latitudes refer to the reference ellipsoid and not the Earth.

Three different latitudes: the geodetic (or geographic) latitude (f ), the astronomic latitude (F) and the geocentric latitude (f ' ).
2.2 3D geographic coordinates (f, l, h)
3D geographic coordinates (f, l, h) are obtained by introducing the ellipsoidal height h to the system. The ellipsoidal height (h) of a point is the vertical distance of the point in question above the ellipsoid. It is measured in distance units along the ellipsoidal normal from the point to the ellipsoid surface. 3D geographic coordinates can be used to define a position on the surface of the Earth (point P in figure below).
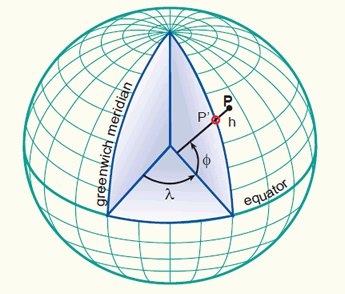
The latitude (f ) and longitude (l) angles and the ellipsoidal height (h) represent the 3D gegraphic coordinate system.
2.3 Geocentric coordinates (X,Y,Z)
An alternative method of defining a 3D position on the surface of the Earth is by means of geocentric coordinates (x,y,z), also known as 3D Cartesian coordinates. The system has its origin at the mass-centre of the Earth with the X- and Y-axes in the plane of the equator. The X-axis passes through the meridian of Greenwich, and the Z-axis coincides with the Earth's axis of rotation. The three axes are mutually orthogonal and form a right-handed system. Geocentric coordinates can be used to define a position on the surface of the Earth (point P in figure below).
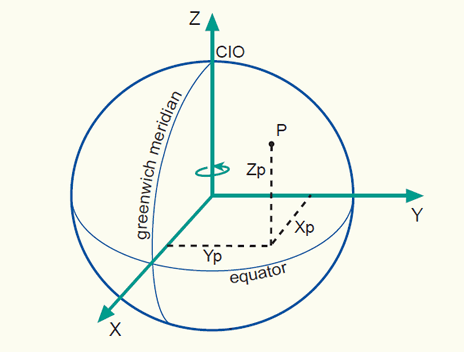
An illustration of the geocentric coordinate system
It should be noted that the rotational axis of the Earth changes its position over time (referred to as polar motion). To compensate for this, the mean position of the pole in the year 1903 (based on observations between 1900 and 1905) has been used to define the so-called 'Conventional International Origin' (CIO).
2.4 2D Cartesian coordinates (X,Y)
A flat map has only two dimensions: width (left to right) and length (bottom to top). Transforming the three dimensional Earth into a two-dimensional map is subject of map projections and coordinate transformations (section 4 and 5). Here, like in several other cartographic applications, two-dimensional Cartesian coordinates (x, y), also known as planar rectangular coordinates, are used to describe the location of any point in a map plane, unambigiously.
The 2D Cartesian coordinate system is a system of intersecting perpendicular lines, which contains two principal axes, called the X- and Y-axis. The horizontal axis is usually referred to as the X-axis and the vertical the Y-axis (note that the X-axis is also sometimes called Easting and the Y-axis the Northing). The intersection of the X- and Y-axis forms the origin. The plane is marked at intervals by equally spaced coordinate lines, called the map grid. Giving two numerical coordinates x and y for point P, one can now precisely and objectively specify any location P on the map.
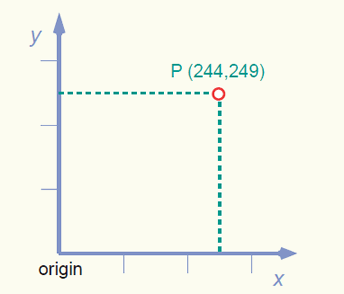
An illustration of the 2D Cartesian coordinate system.
Normally, the coordinates x = 0 and y = 0 are given to the origin. However, sometimes large positive values are added to the origin coordinates. This is to avoid negative values for the x and y coordinates in case the origin of the coordinate system is located inside the area of interest. The point which then has the coordinates x = 0 and y = 0 is called the false origin.
An example is the map coordinate system used in the Netherlands. It is called Rijksdriehoekstelsel (RD). The system is based on an azimuthal stereographic projection (section 4 on map projections) and the Bessel ellipsoid is used as reference surface. The origin of the coordinate system has been shifted (false origin) from the projection centre (Amersfoort) towards the south-west to avoid negative coordinates inside the country (figure below).
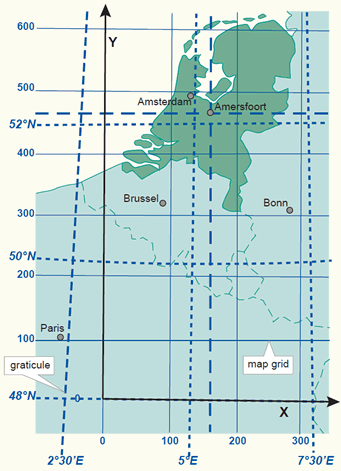
The coordinate system of the Netherlands represented by the map grid and graticule. The origin of the coordinate system has been shifted (false origin) from the projection centre (Amersfoort) towards the South-West.
The grid on a map represents lines having constant 2D Cartesian coordinates (x,y). It is almost always a rectangular system and is used on large and medium scale maps to enable detailed calculations and positioning. The map grid is usually not shown on small scale maps (about one to a million or smaller). Scale distortions that result from transforming the Earth’s curved surface to the map plane are so great on small-scale maps that detailed calculations and positioning are difficult.
The graticule on a map represents the projected position of the geographic coordinates (f,l) at constant intervals, or in other words the projected position of selected meridians and parallels. The shape of the graticule depends largely on the characteristics of the map projection used and the scale of the map (figure below).

The world mapped in the Transverse Mercator projection with a 15 degrees graticule.
The map sheet limit or neat line (the line enclosing the mapped area) can either be formed by the outline of the grid or by the outline of the graticule. The grid as outline of the mapped area has the advantage of being rectangular, hence the map face of each map sheet will be exactly the same size, allowing a completely uniform arrangement of the marginal information. This type of sheet index system is used for topographic mapping of the Netherlands. The graticule as outline of the mapped area might give a curved outline and the size of the mapped area, covered by a particular geographic coordinate unit (e.g. 15' of latitude by 15' of longitude), will vary according to the location on Earth and the projection system. However, it shows immediately the extent of the area in the geographic system.
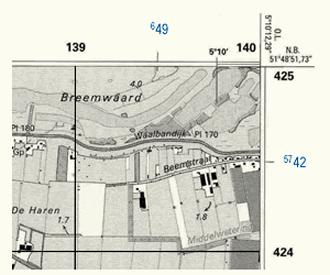
Two different map grids are shown on the 1:25,000 topographic maps of the Netherlands. The grid lines and the coordinate values of the Dutch RD system are portrayed in black. The coordinate values of the UTM grid are portrayed in blue. The geographic coordinates are shown at every 5 minutes and at the corners of the map.
Grid and graticule spacings on a map vary depending on the scale of the map. The topographic maps of the Netherlands at scale 1:25,000 show grid lines at every kilometer and the graticule lines (or ticks) are given at every 5 minutes (figure above).
2.5 2D polar coordinates (a,d)
Another possibility of defining a point in a plane is by polar coordinates (a,d). This is the distance d from the origin to the point concerned and the angle a between a fixed (or zero) direction and the direction to the point. The angle a is called azimuth or bearing and is measured in a clockwise direction. It is given in angular units while the distance d is expressed in length units.
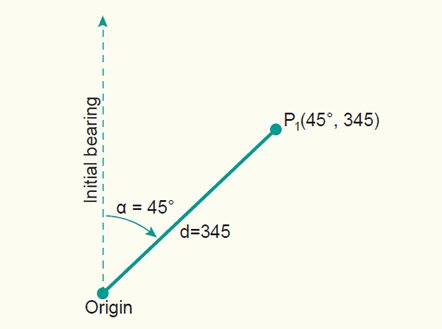
An illustration of the 2D Polar coordinate system.
Bearings are always related to a fixed direction (initial bearing) or a datum line. In principle, this reference line can be chosen freely. However, in practice three different directions are widely used: True North, Grid North and Magnetic North (FAQ's nr. 30). The corresponding bearings are called: true (or geodetic) bearing, grid bearing and magnetic (or compass) bearing.
Polar coordinates (a,d) are often used in land surveying. For some types of surveying instruments it is advantageous to make use of this coordinate system. The development of precise remote distance measurement techniques has led to the virtually universal preference for the polar coordinate method in detailed surveys.
The transformation of polar coordinates (a,d) into Cartesian coordinates (x,y) is done when field measurements, angular and distance measurements are transformed into map coordinates. The equation for this transformation is:
The inverse equation is:
A more realistic case makes use of a translation and a rotation to transform one system to the other.
2.6 Main references
R.A. Knippers. Geometric Aspects of Mapping. Non-published educational notes. ITC, Enschede, 1999.
A. Mehlbreuer. Geometric Fundamentals of Mapping. Non-published educational notes. ITC, Enschede.